The nonlinear behaviour of a ducted premixed flame (a numerical study)
Duration: 27 mins 42 secs
Share this media item:
Embed this media item:
Embed this media item:
About this item
| Description: |
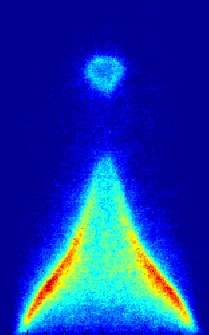
When a flame is placed in a duct, acoustic oscillations couple with heat release oscillations and can grow to high amplitudes. This presentation shows the behaviour of a numerical model of such a coupled thermoacoustic system. The model displays elaborate nonlinear behaviour, featuring oscillations that are periodic, quasi-periodic, frequency-locked, or chaotic. At least two routes to chaos are seen: the period-doubling route and the Ruelle-Takens-Newhouse scenario. This study complements recent experiments by Kabiraj and Sujith (IIT Madras) by providing a reduced order model of a system with approximately 5000 degrees of freedom that captures much of the complex nonlinear dynamics observed in experiments
|
|---|
| Created: | 2013-01-04 13:02 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Collection: | Matthew Juniper conference presentations | ||||||||
| Publisher: | University of Cambridge | ||||||||
| Copyright: | Dr Matthew Juniper | ||||||||
| Language: | eng (English) | ||||||||
| Keywords: | acoustics; combustion; instability; non-linear; chaos; flames; gas turbines; oscillations; | ||||||||
| Credits: |
|
||||||||
| Abstract: | Thermoacoustic systems exhibit self-excited oscillations due to resonant coupling between unsteady heat release and acoustic waves. Recent experimental studies have shown that these oscillations are often non-periodic. In this presentation we create a numerical model of a ducted slot-stabilized premixed flame and investigate the bifurcations that occur as the position of the flame in the duct is varied. The system undergoes transition to limit cycle oscillations via a subcritical Hopf bifurcation followed by subsequent bifurcations that lead to quasi-periodic, period- two, frequency-locked as well as chaotic oscillations. For certain parameter ranges several stable oscillating solutions exist and the ultimate state reached depends on the initial conditions. Hence mode-switching and hysteresis is evident. Examining the time series also shows that the system often traverses through several intermediate unstable states before reaching its final stable state. Furthermore, at least two routes to chaos are established for this system: the period-doubling route and the Ruelle-Takens-Newhouse scenario. These are corroborated by analyses of the power spectra of pressure and velocity. This study complements recent experiments by Kabiraj and Sujith (IIT Madras) by providing a reduced order model of a system with approximately 5000 degrees of freedom that captures much of the complex nonlinear dynamics observed in the laboratory. |
|---|---|
Available Formats
| Format | Quality | Bitrate | Size | |||
|---|---|---|---|---|---|---|
| MPEG-4 Video | 480x360 | 422.44 kbits/sec | 85.71 MB | View | Download | |
| WebM | 360x360 | 150.86 kbits/sec | 30.63 MB | View | Download | |
| iPod Video | 480x360 | 286.54 kbits/sec | 58.14 MB | View | Download | |
| QuickTime | 384x288 | 126.58 kbits/sec | 25.68 MB | View | Download | |
| MP3 | 44100 Hz | 249.86 kbits/sec | 50.72 MB | Listen | Download | |
| Auto * | (Allows browser to choose a format it supports) | |||||